그래프 (Graph)
👉 비선형적 자료구조
👉 정점(vertex)과 정점을 연결하는 간선(edge)을 포함
👉 연결에 일정한 패턴을 이루고 있지 않음
👉 그래프는 비어있을 수 있음
👉 그래프는 순환(Cycle) 혹은 비순환(Acycle)
❗️순환(Cycle) : 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
무방향 그래프 (Undirected Graph)
: 두 정점를 연결하는 간선의 방향이 없는 그래프
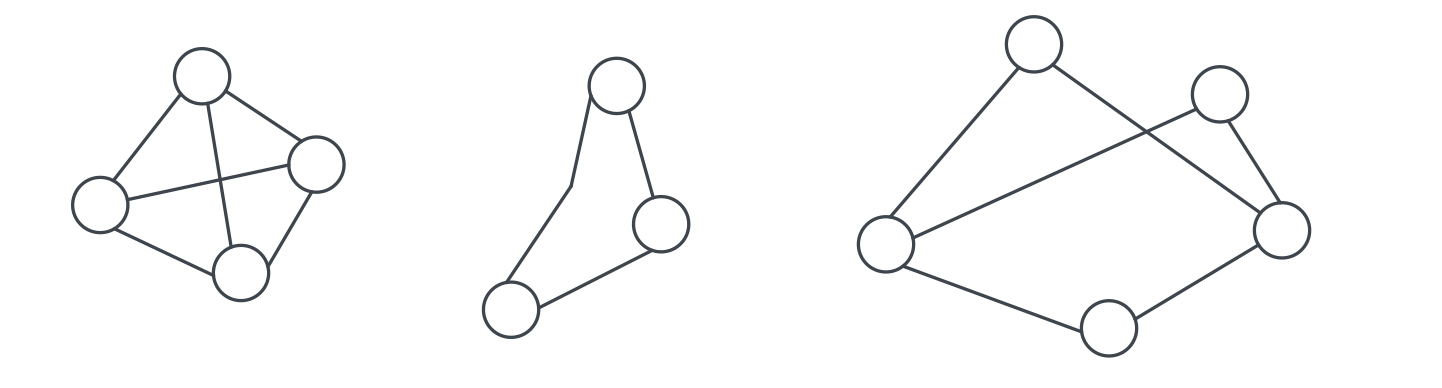
방향 그래프 (Directed Graph)
: 두 정점 연결하는 간선의 방향이 있는 그래프
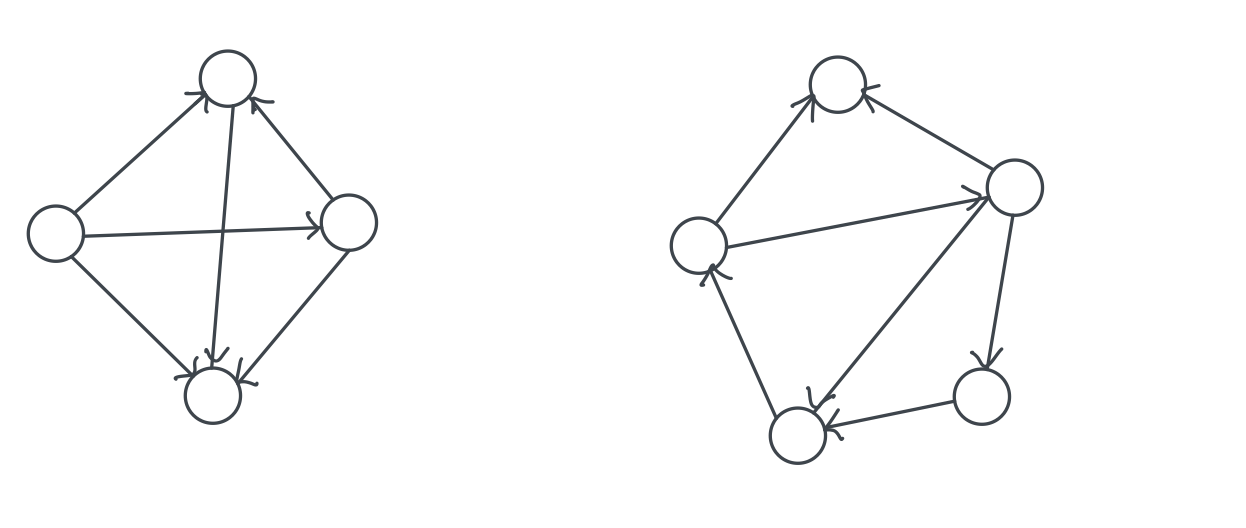
완전 그래프 (Complete Graph)
: 모든 정점들 사이에 1:1로 직접 연결된 간선을 갖는 그래프
👉 정점이 n개인 무방향 그래프인 경우, 최대 간선 수 = n(n - 1)/2

부분 그래프 (Subgraph)
: 원래의 그래프에서 일부의 정점이나 간선을 제외하여 만든 그래프
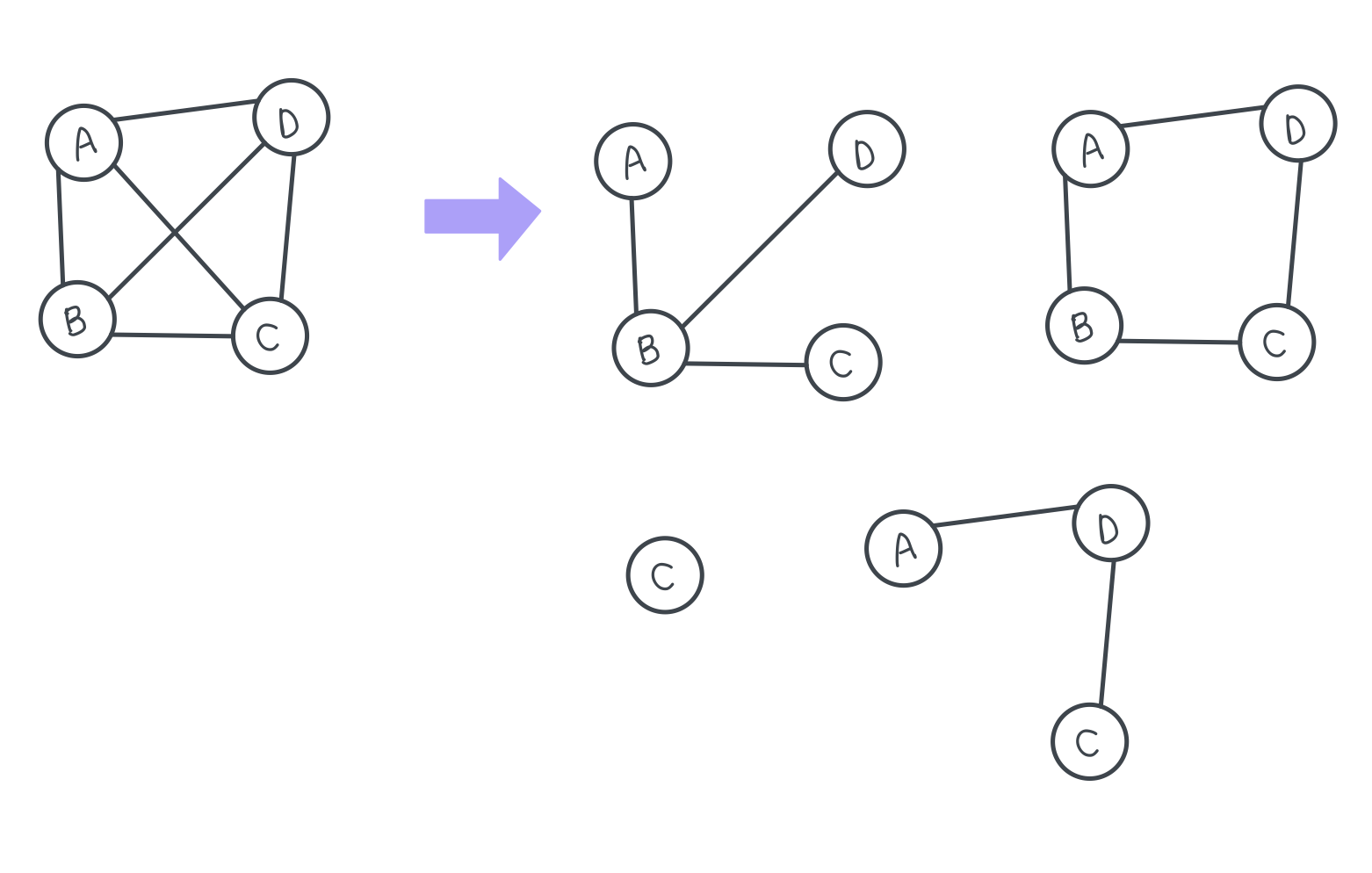
가중 그래프 (Weight Graph)
: 노드를 연결하는 링크에 가중치(weight)를 할당한 그래프
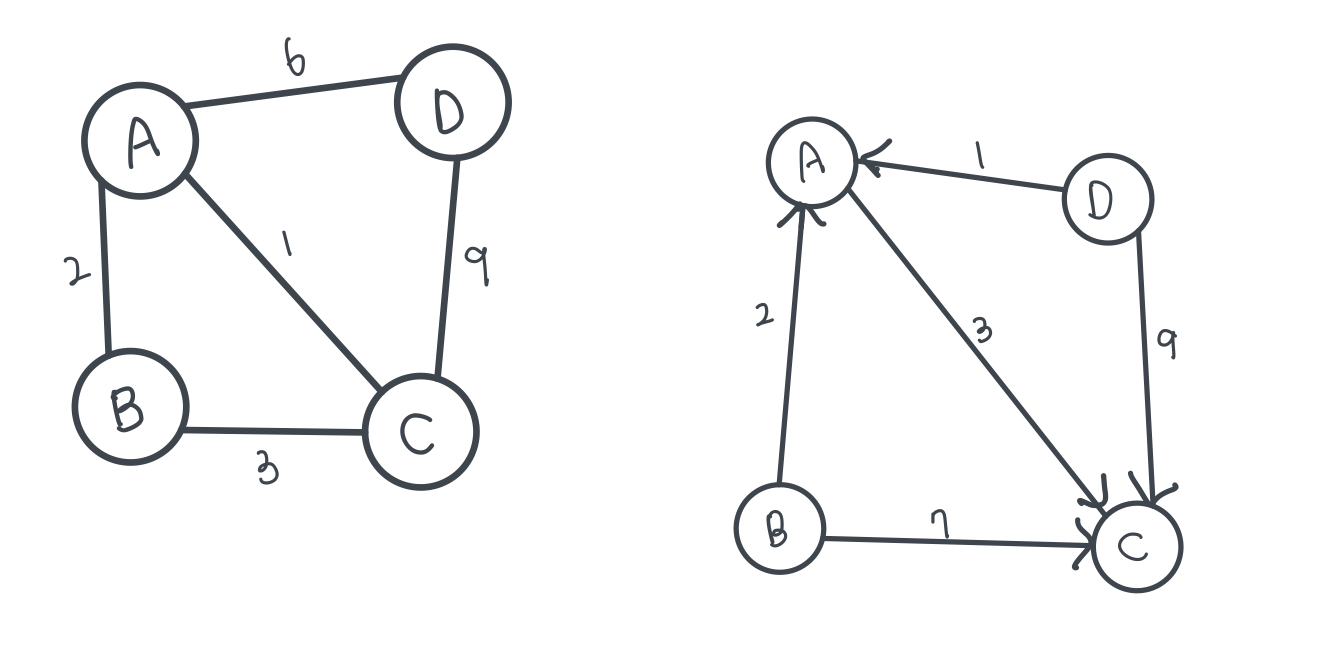
그래프의 표현 방법
1. 인접 행렬 (Adjacency Matrix)
👉 그래프의 정점 간의 연결 관계를 2차원 배열로 표현
👉 N개의 정점을 가진 그래프는 각 정점에 대한 행과 열을 나타내므로 n x n 행렬
👉 두 정점이 인접되어 있으면 1(or True), 인접되어 있지 않으면 0(or False)로 표현
🙋🏻♀️ 그래프 내에 많은 숫자의 간선을 가지고 있는 밀집 그래프(Dense Graph)일 경우
✔️ 장점
구현이 쉽고, 특정 노드와 특정 노드의 인접 여부 확인이 빠름.
✔️ 단점
특정 정점과 인접한 정점을 알고자 할 때 모든 간선을 확인해야 함. 일부 간선으로만 이루어진 그래프라도 n^2개의 메모리 공간이 필요하므로 메모리 낭비가 될 수 있음.
2. 인접 리스트 (Adjacency List)
👉 그래프의 정점 간의 연결 관계를 연결 리스트를 이용하여 표현
👉 특정 정점과 연결된 정점을 연결 리스트에 저장
🙋🏻♀️ 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph)일 경우
✔️ 장점
인접한 정점들만 연결 리스트에 저장하므로 간선의 개수에 비례하는 메모리만 사용. 특정 정점과 인접한 정점을 알고 싶을 때 효율적.
✔️ 단점
특정 정점과 특정 정점이 연결되어 있는지 여뷰를 판단하고자 할 때, 연결 리스트를 순차적으로 확인해야 함.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] priority_queue 컨테이너_C++ (0) | 2022.05.10 |
|---|---|
| [자료구조] 우선순위 큐 와 힙의 차이점 (0) | 2021.01.23 |
| [자료구조] map 컨테이너_C++ (0) | 2021.01.23 |
| [자료구조]이진 힙 (Binary Heap) (0) | 2021.01.12 |
| [자료구조] 트리 (Tree) (0) | 2021.01.03 |